方阵的行列式的性质(行列式,为什么?)
行列式的定义:
设 V 是域K上的 n维线性空间,若 V 上的 n重函数 det:(V)ⁿ→K , 对于 任意一个参数 vᵢ,都满足线性性质:
- det(..., vᵢ + v, ...) = det(..., vᵢ, ...) + det(..., v, ...),(v ∈ V);
- det(.., kvᵢ, ...) = k det(.., vᵢ, ...) , (k ∈ K);
则称 det 为线性函数,若 det 还满足行列式性质:
- det 是反对称的,即,det(..., vᵢ, ..., vⱼ, ...) = -det(..., vⱼ, ..., vᵢ, ...) ;
- 对于 V 的 自然标准单位正交基 e₁, ..., eₙ,有 det(e₁, ..., eₙ)=1;
则 称 det 为 行列式,并记,
| v₁ |
| ... | =det(v₁, ..., vₙ)
| vₙ |
◈◈◈◈◈◈
行列式的解析式推导:
以 K = ℝ ,V = ℝⁿ 为例, 此时,
e₁=(1, 0, ..., 0), ..., eₙ=(0, ..., 0, 1)
于是任意向量 v=(a₁, ..., aₙ) 可线性表示为,
v=a₁e₁+...+aₙeₙ
定义投影函数,
e¹(v)=a₁, ..., eⁿ(v)=aₙ
对于 任意一组向量
v₁=a₁₁e₁+...+a₁ₙeₙ, ...,vₙ=aₙ₁e₁+...+aₙₙeₙ,
根据线性性质,有,
det(v₁, ..., vₙ)=∑ᵢ₁,...,ᵢₙ₌₁ⁿa₁ᵢ₁⋅⋅⋅aₙᵢₙdet(eᵢ₁, ..., eᵢₙ)=∑ᵢ₁,...,ᵢₙ₌₁ⁿdet(eᵢ₁, ..., eᵢₙ)a₁ᵢ₁⋅⋅⋅aₙᵢₙ=∑ᵢ₁,...,ᵢₙ₌₁ⁿdet(eᵢ₁, ..., eᵢₙ)eⁱ¹(v₁)⋅⋅⋅eⁱⁿ(vₙ)
对于任意一组线性函数 f₁, ..., fₙ:V→K,定义张量积,
(f₁⊗⋅⋅⋅⊗fₙ)(v₁, ..., vₙ)=f₁(v₁)⋅⋅⋅fₙ(vₙ)
则有,
det=∑ᵢ₁,...,ᵢₙ₌₁ⁿdet(eᵢ₁, ..., eᵢₙ) eⁱ¹⊗⋅⋅⋅⊗eⁱⁿ
再 根据 反对称性,可推导出:
- det(eᵢ₁, ..., eᵢₙ) ≠ 0 当且仅当 i₁ ≠ ... ≠ iₙ
此时,i₁,...,iₙ 是 N={1, ..., n} 的一个全排列,于是存在 N 上的 置换 s ∈ Sₙ,使得,
i₁=s(1),...,iₙ =s(n)
进而有,
det=∑s ∈ Sₙ det(eₛ₍₁₎, ..., eₛ₍ₙ₎) eˢ⁽¹⁾⊗⋅⋅⋅⊗eˢ⁽ⁿ⁾
又 根据 行列式性质,有,
det(eₛ₍₁₎, ..., eₛ₍ₙ₎)=(-1)ᴺˢdet(e₁, ..., eₙ)=(-1)ᴺˢ·1=(-1)
其中,Nₛ=N(s(1), ..., s(n)) 表示 s(1), ..., s(n) 的逆序数,这样最终就得到行列式的解析式:
det=∑s ∈ Sₙ (-1)ᴺˢ eˢ⁽¹⁾⊗⋅⋅⋅⊗eˢ⁽ⁿ⁾
写成大家熟悉的形式就是:
| a₁₁, ..., a₁ₙ |
| ..., ..., ... | =∑ₚ₁,...,ₚₙ (-1)ᴺ⁽ᵖ¹’¨’ᵖⁿ⁾ aₚ₁⋅⋅⋅aₚₙ
| aₙ₁, ..., aₙₙ |
◈◈◈◈◈◈
最后,众所周知:
- n重线性函数 就是 n阶协变张量,
于是我们有如下总结:
- n维线性空间 V上的 n阶行列式 det 就是,使得 det(E)=1 的 V 上的 反对称 n阶逆变 张量。
这里,
┌ e₁ ┐ ┌ 1, 0, ..., 0 ┐
│ ... │= │ ... ... ... .... │ = E
└ eₙ ┘ └ 0, ...., 0, 1 ┘
是 单位矩阵。
行列式的 性质 是怎么来的?
实际上,n阶 行列式的 几何意义是
- 以n个参数向量为边构成的 n维超平行六面体的 有向体积;
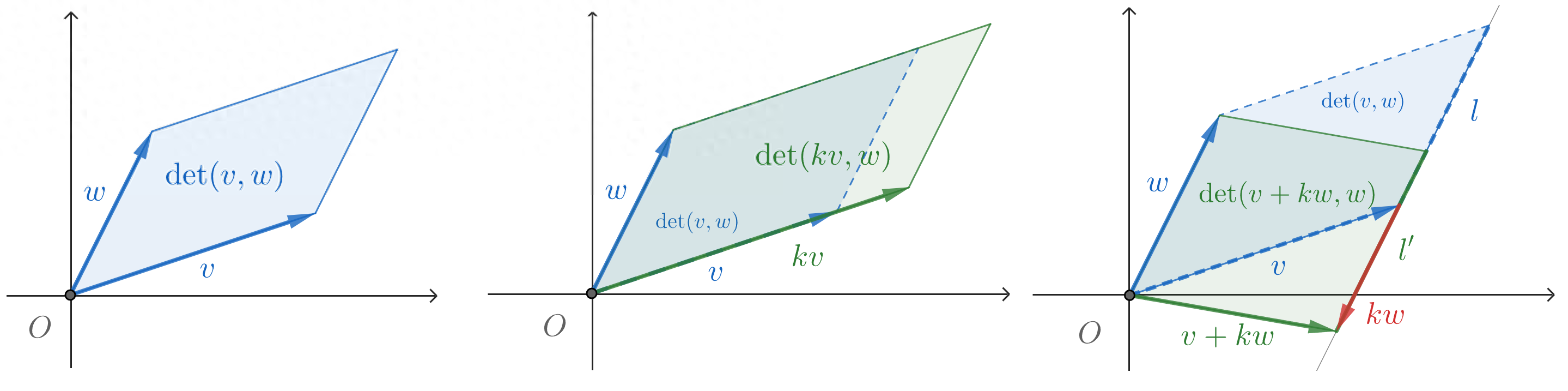
以 n = 2 为例,则 行列式 det(v, w) 即为上图的平行四边形面积,此时以我们初中《平面几何》的经验容易得到如下结论【注:以下只对参数v进行推导,而参数w类似,不加累述】:
- 缩放性:将 一个边缩放 k 倍,则 平行四边形面积 也跟着 缩放k倍,即,det(kv, w) = kdet(v, w),这就是线性性质2;
- 平移不变性:将 一个边沿着所在直线平移,则 平行四边形面积 不变,设 平移的是 w 的对边 l,平移向量是 kw,则平移后 v 边变为 v + kw,于是我们有 det(v, w) = det(v + kw, w);
这样我们就得到了 平行四边形面积 的两大公理,通过这个 两大公理,我们可以推导出:
- 线性性质1:
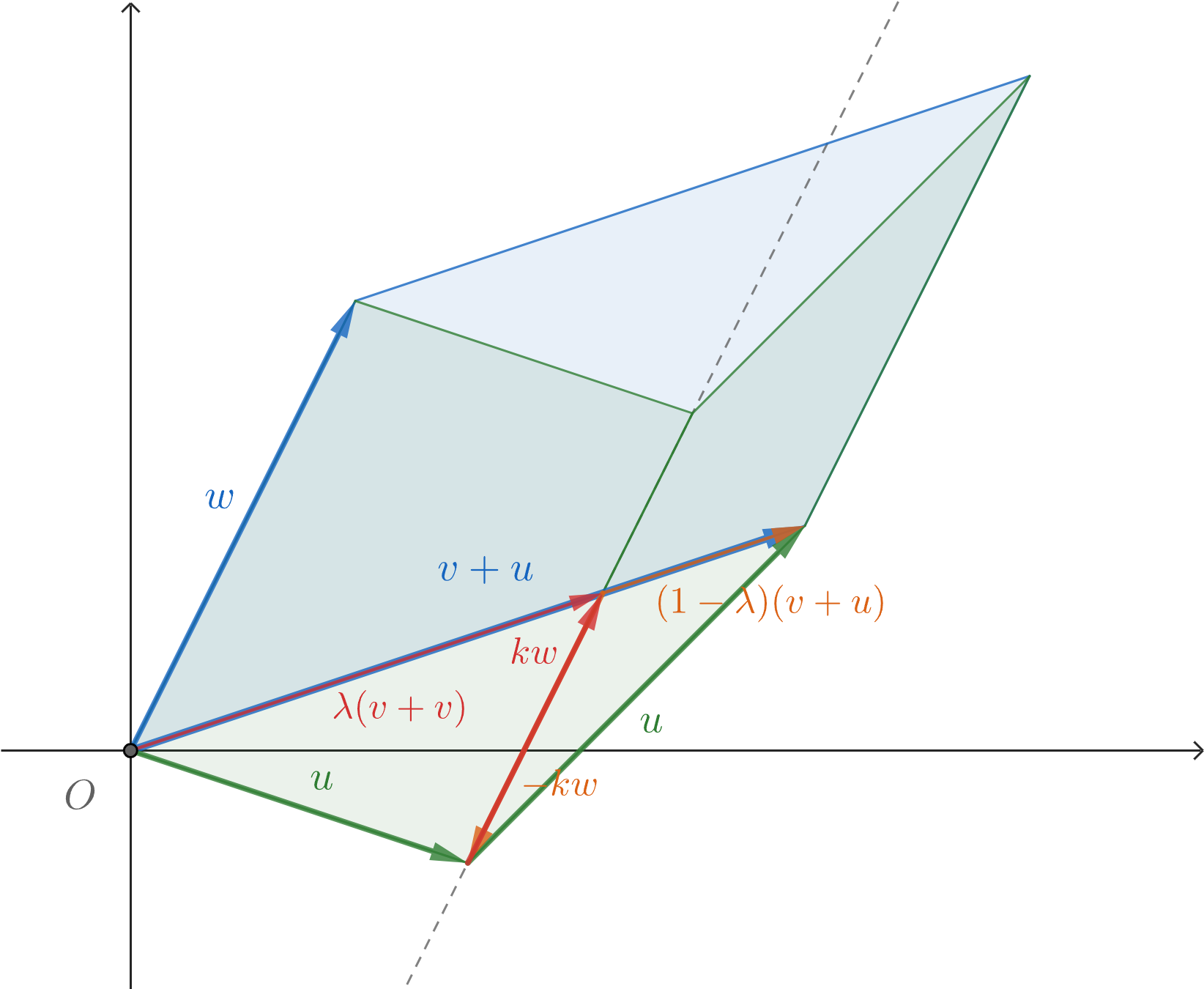
如图,有,
det(v, w) + det(u, w) = det(v + kw, w) + det(-kw + u , w) = det(λ(v + u), w) + det((1-λ)(v + u) , w) = λdet(v + u, w) + (1-λ)det(v + u , w) = (λ + (1-λ))det(v + u, w) = det(v + u, w)
即得到,
det(v + u, w) = det(v, w) + det(u, w)
- 反对称性:
det(u, u) = det(u + (-ku), u) = det(0, u) = det(0u, u) = 0det(u, u) = 0
即得到,
det(u, u)= 0 ①
再 根据 线性性质1 有,
0 = det(v+w, v+w) = det(v+w, v+w) = det(v, v+w) + det(w, v+w) = det(v, v) + det(v, w) + det(w, w) + det(w, v) = 0 + det(v, w) + 0 + det(w, v) = det(v, w) + det(w, v)
即得到,
det(w, v) = -det(w, v)
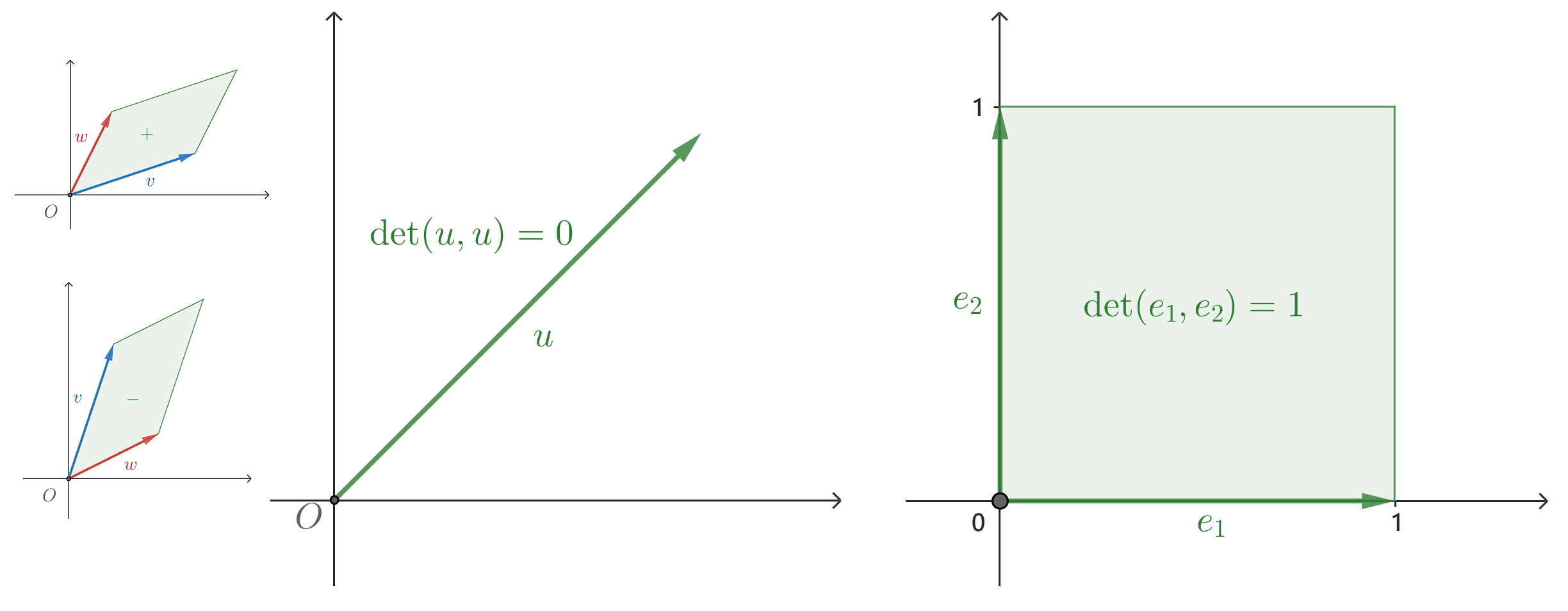
最后,如图,单位面积自然是1,即,
det(e₁, e₂) = 1
上面的推导说明,反对称性 可以通过 性质① 得到,而反过来 由反对称性有,
det(u, u) = -det(u, u) ⇒ 2det(u, u) = 0 ⇒ det(u, u) = 0
这样就证明了,反对称性 和 性质① 等价,于是可将 行列式性质 中的 反对称性 替换为 性质①。另外,在满足线性性质的情况下,也可以由 性质① 得到 平移不变性,推导过程如下,
det(v + kw, w) = det(v, w) + det(kw, w) = det(v, w) + kdet(w, w) = det(v, w) + k0 = det(v, w)
【注: n > 2 的情况 和上面类似,这里不在累述】
BTW:
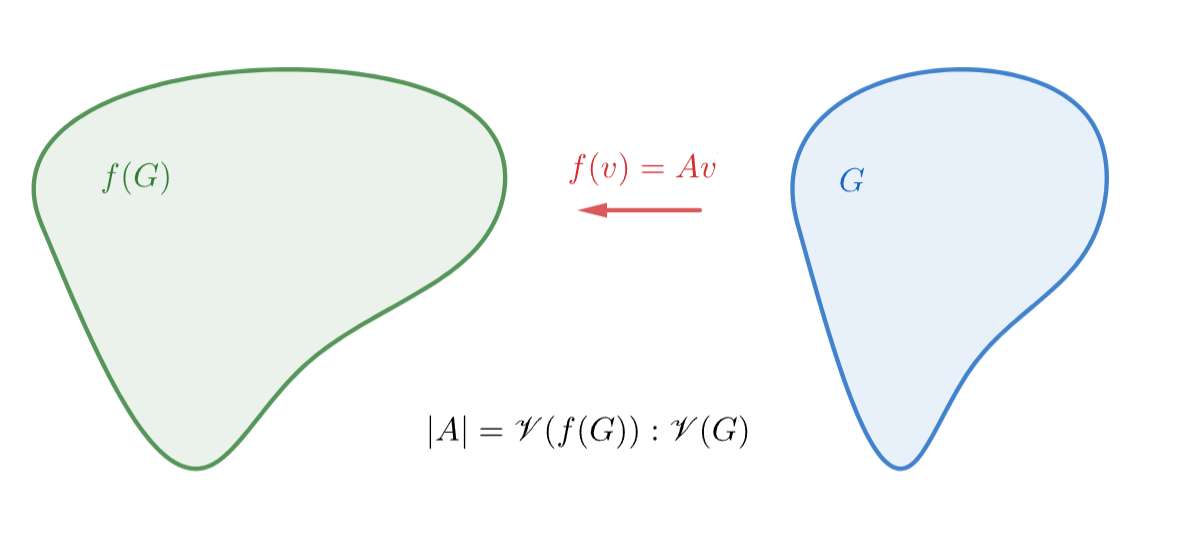
我们知道 V 上的 线性变换 f: V→V,在 V 确定基之后 与 V 上的 唯一 n阶方阵 A 对应,即有,f(v) = Av,此时,若设 V 中的 超几何体 G 被 f 变换为 f(G),则 行列式的 |A| 的意义就是,
|A| = f(G)的超体积 : G的超体积 ②
考虑,椭圆,
x²/a² + y²/b² = 1
它可以看成 是 单位圆,
x² + y² = 1
在 方阵,
┌ a 0 ┐ = A
└ 0 b ┘
对应的线性变换下得到的,性质 ② 有,
|A| = 椭圆面积 : 单位圆面积
而,
|A| = ab,单位圆面积 = π
于是得到,
椭圆面积 = abπ
